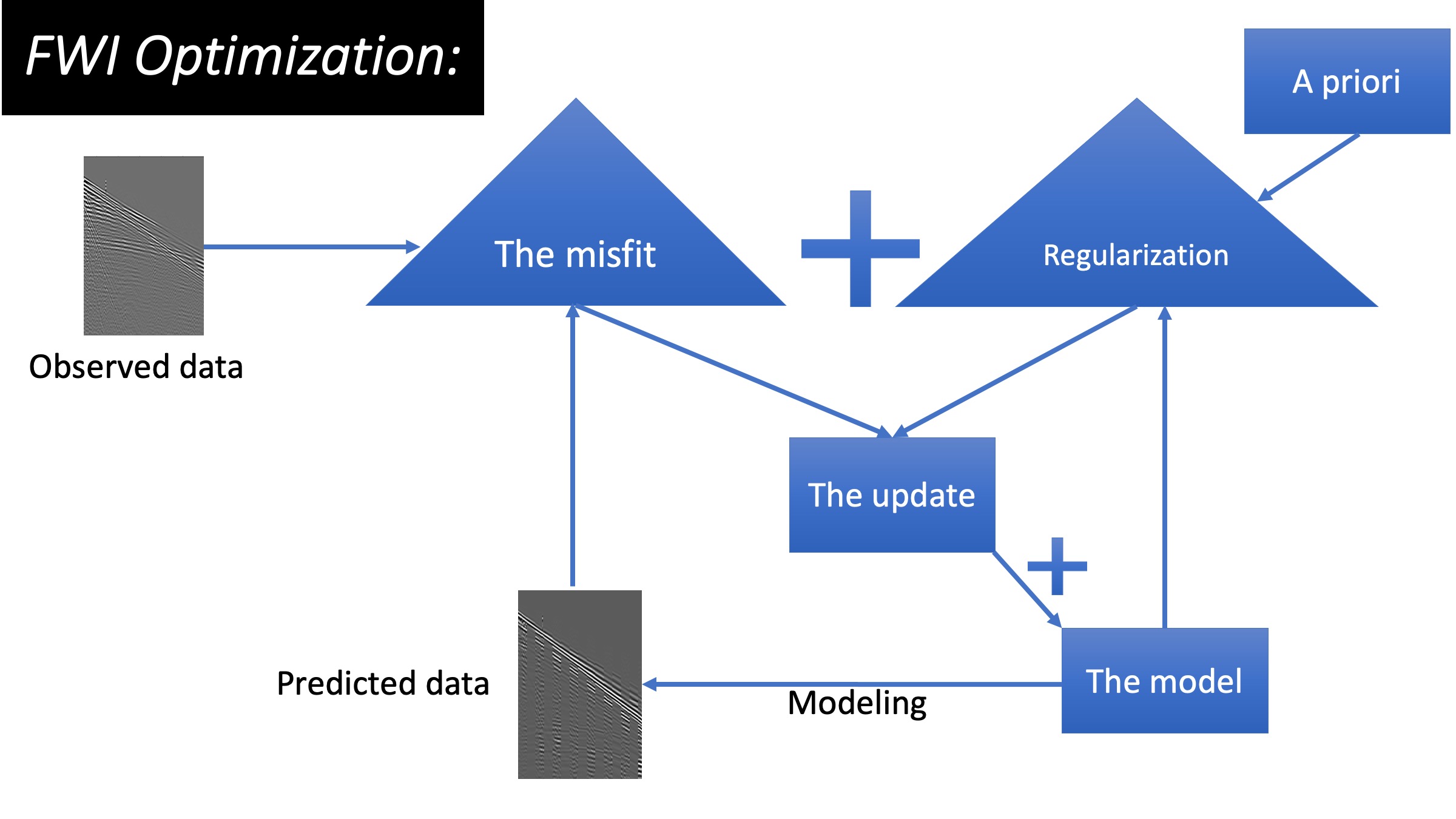
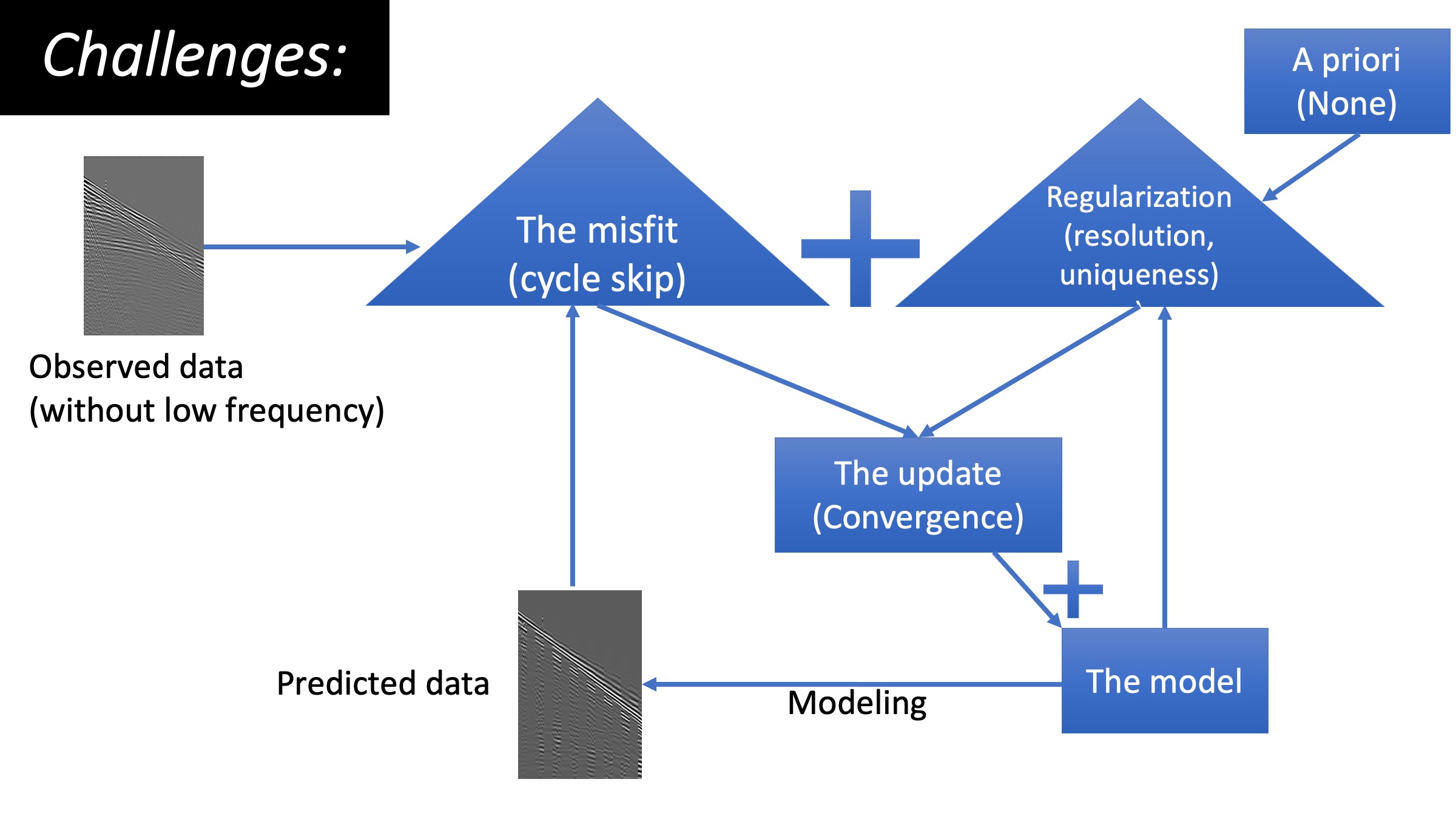
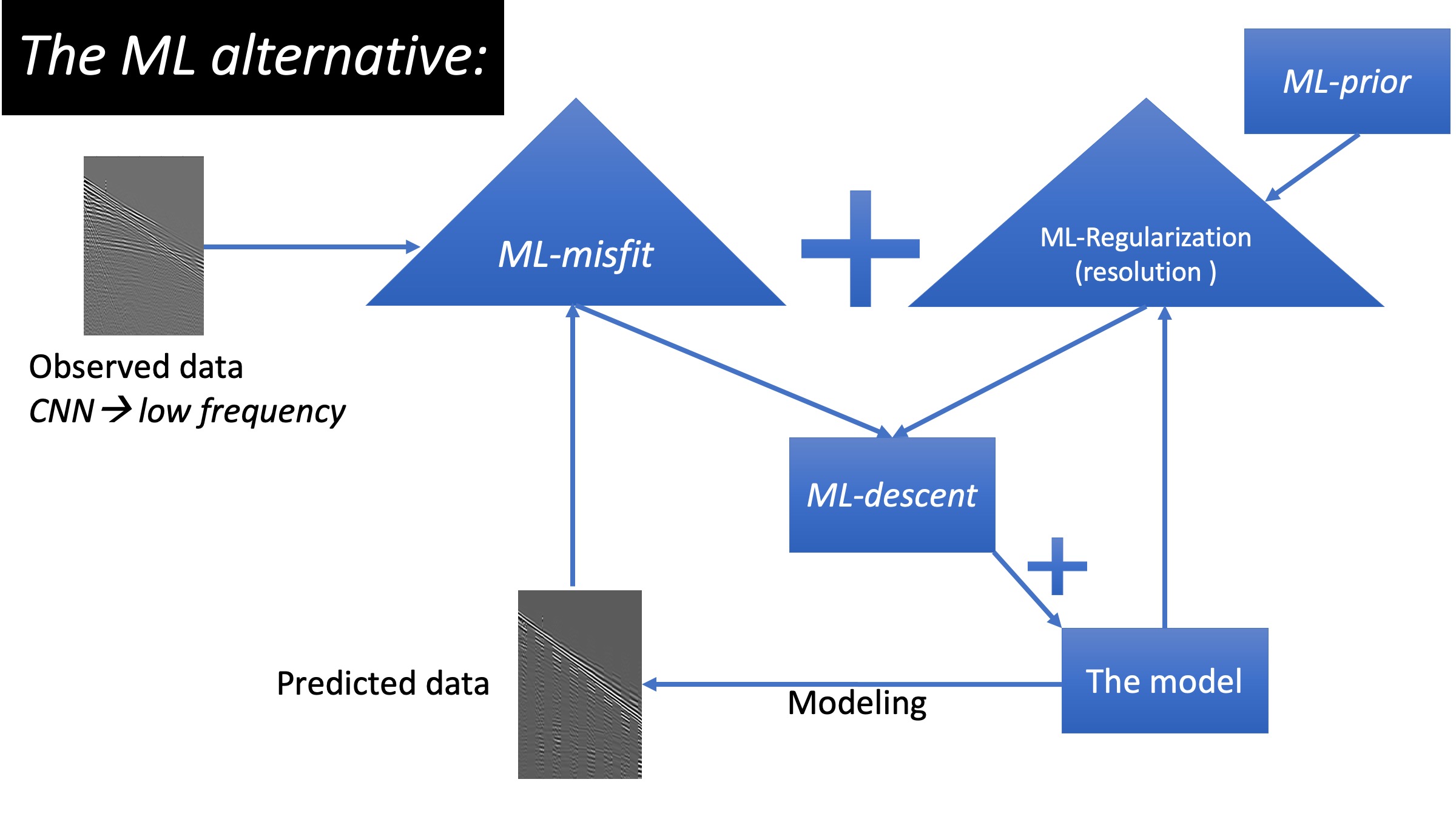
The shift to ML solutions for Full waveform inversion in three diagrams

Below, we address the challenges concerning the three main (important) components of the waveform inversion machinery using ML:
  1. The objective function: we train a neural network (NN) to replace the classic misfit, we refer to it as the ML-misfit.
  2. The regularization: we train an NN to map information from a well to act as an a priori for FWI, we refer to as the ML-prior.
  3. The update: we train an NN to be an optimal conditioner to the gradient, we refer to it as the ML-descent.

 

The ML-misfit

Based on a recently introduced machine-learned misfit function, entitled ML-misfit (Sun and Alkhalifah, 2020a), we provide a robust metric for a misfit that reduces cycle skipping in full-waveform inversion (FWI). The resulting ML-misfit, the same as any hand-crafted misfit functions (loss, metric), takes in two vectors as input, representing the predicted and measured data, and outputs a scalar value. Inspired by the optimal transport of the matching filter (OTMF) misfit function, the neural network of the ML-misfit is designed specially to compare the mean and variance of the similarity distribution between the predicted and measured data. Based on the concept of meta-learning, we train the ML-misfit using many FWI tasks by minimizing a meta-loss defined to be the accumulated model difference between the true and inverted ones.

The ML-prior

This regularization technique (Li et al., 2020) combines the seismic and well log data, to help improve the resolution of elastic waveform inversion (EFWI). We use deep neural networks to learn the mathematical relationship between some selected features of the inverted model and the facies interpreted from well logs. The selected features are the means and variances of the well velocities computed within a Gaussian window. Using deep fully connected layers, we train our neural network to identify the relation between the mean and variances at the well, with the inverted velocity model from an initial EFWI application. The network is used to map the mean and variance extracted from the well to the rest of the model domain. We then perform another EFWI in which we fit the predicted data to the observed one, as well as, fit the model over a Gaussian window to the predicted mean and variances.

The ML-descent

A recently developed ML-descent methodology utilizes both an auto-encoder and a recurrent neural network (RNN) to use the history information of gradients to provide a better update (Sun and Alkhalifah, 2020b), like the well-known L-BFGS. However, unlike L-BFGS, our network learns from the data and learns to optimize the update from the data. The input to the RNN are the gradients at each iteration and the output is the update, both in the latent space. The network trained on patches from the Marmousi model performed much better than L-BGFS on the overthrust model. We converge to a high-resolution model with fewer iterations.

 

 

 

Figures_for_Research0_Tariq_C

References

Li Y., Alkhalifah T., and Zhang Z., (2020), "High-Resolution Regularized Elastic Full Waveform Inversion Assisted by Deep Learning", Conference Proceedings, 82nd EAGE Annual Conference & Exhibition Workshop. DOI: 10.3997/2214-4609.202010281.

Sun B., and Alkhalifah T., (2020a), "ML-Misfit: Learning a Robust Misfit Function for Full-Waveform Inversion Using Machine Learning", King Abdullah University of Science and Technology, arxiv:2002.03163.

Sun B., and Alkhalifah T., (2020b), "ML-descent: an optimization algorithm for FWI using machine learning", GEOPHYSICS: accepted. DOI:10.1190/geo2019-0641.1.

Li Y., Alkhalifah T., and Zhang Z., (2020), "High-Resolution Regularized Elastic Full Waveform Inversion Assisted by Deep Learning", Conference Proceedings, 82nd EAGE Annual Conference & Exhibition Workshop. DOI: 10.3997/2214-4609.202010281.

Sun B., and Alkhalifah T., (2020a), "ML-Misfit: Learning a Robust Misfit Function for Full-Waveform Inversion Using Machine Learning", King Abdullah University of Science and Technology, arxiv:2002.03163.

Sun B., and Alkhalifah T., (2020b), "ML-descent: an optimization algorithm for FWI using machine learning", GEOPHYSICS: accepted. DOI:10.1190/geo2019-0641.1.