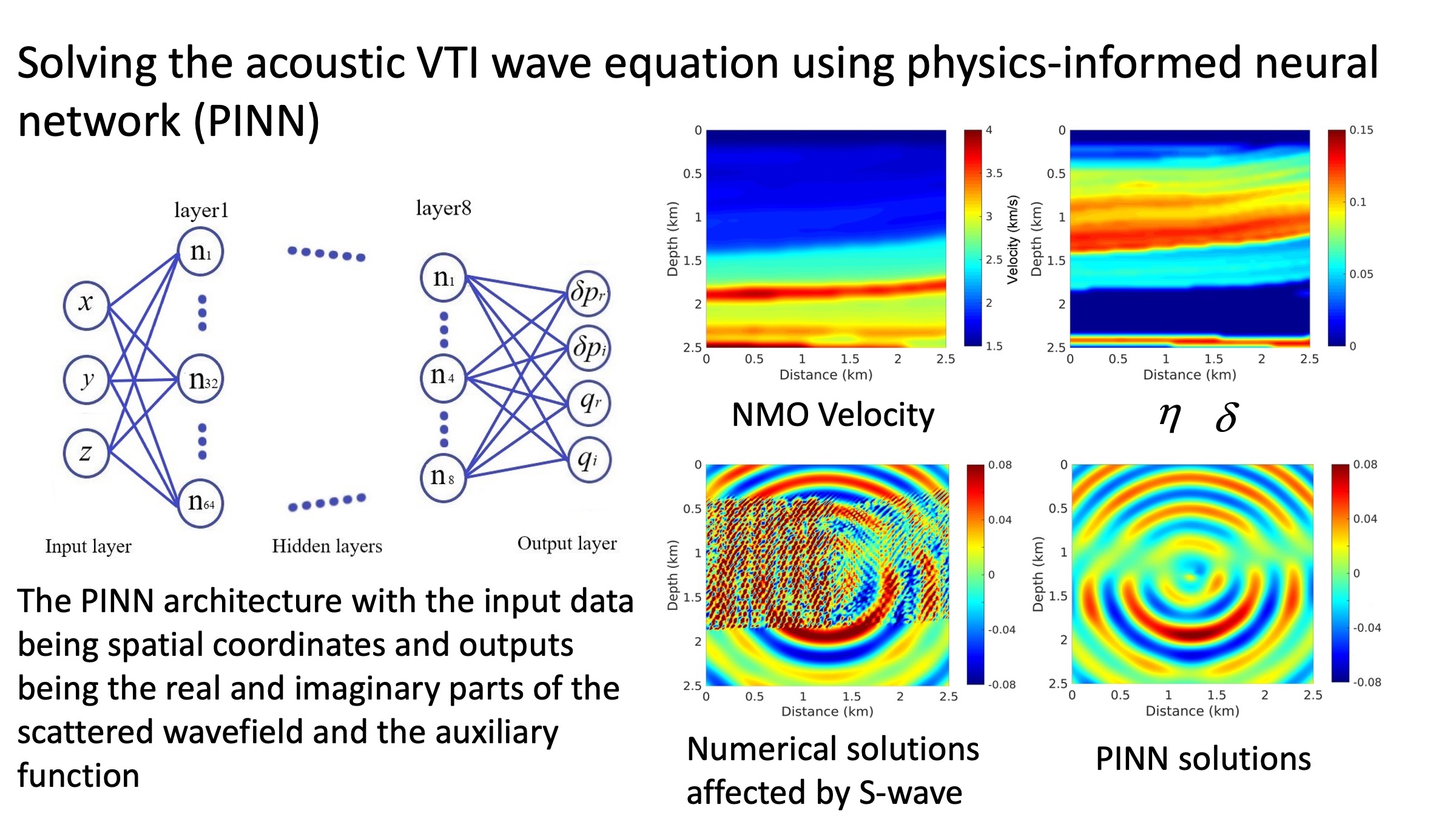
Solving the acoustic VTI wave equation using physics-informed neural network (PINN) (Song et al., 2020)

Frequency-domain wavefield solutions corresponding to the anisotropic acoustic wave equation can be used to describe the anisotropic nature of the Earth. To solve a frequency-domain wave equation, we often need to invert the impedance matrix. This results in a dramatic increase in computational cost as the model size increases. It is even a bigger challenge for anisotropic media, where the impedance matrix is far more complex. In addition, the conventional finite-difference method produces numerical dispersion artifacts in solving acoustic wave equations for anisotropic media.

To address these issues, we use the emerging paradigm of physics-informed neural networks (PINNs) to obtain wavefield solutions for an acoustic wave equation for transversely isotropic (TI) media with a vertical axis of symmetry (VTI). PINNs utilize the concept of automatic differentiation to calculate their partial derivatives, which are free of numerical dispersion artifacts. Thus, we use the wave equation as a loss function to train a neural network to provide functional solutions to the acoustic VTI form of the wave equation. Instead of predicting the pressure wavefields directly, we solve for the scattered pressure wavefields to avoid dealing with the point-source singularity. We use the spatial coordinates as input data to the network, which outputs the real and imaginary parts of the scattered wavefields and auxiliary function. After training a deep neural network (DNN), we can evaluate the wavefield at any point in space almost instantly using this trained NN without calculating the impedance matrix inverse.

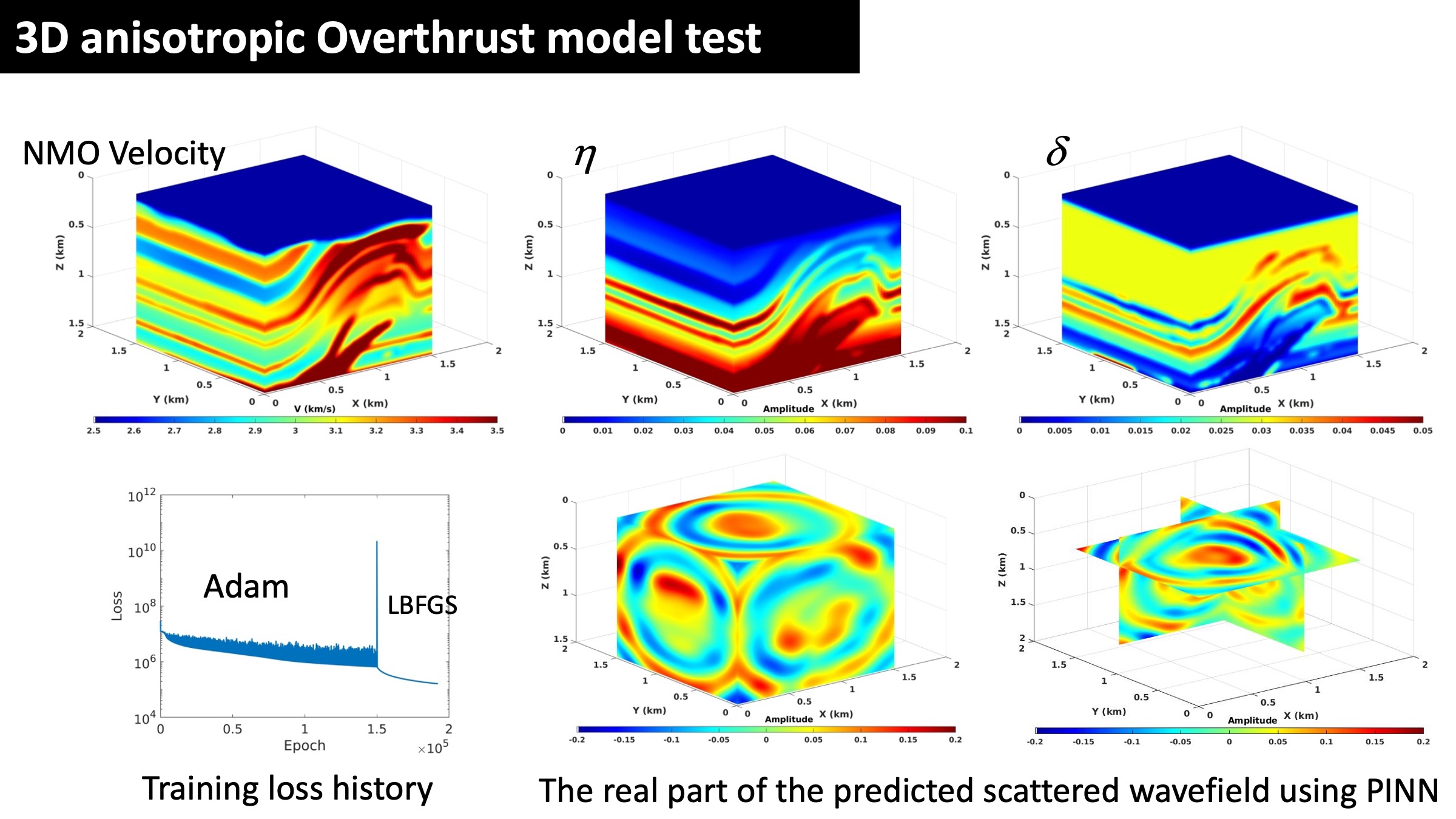
We demonstrate these features on a simple 2D anomaly model and a 2D layered model. Additional tests on a modified 3D Overthrust model and a 2D model with irregular topography further validate the effectiveness of the proposed method.