Predictive uncertainty quantification for Bayesian Physics-Informed Neural Network (PINN) in hypocentre estimation problem (Izzatullah, M., Yildirim, I. E., Waheed, U. B., and Alkhalifah, T., 2022)

Research objectives:

  • To introduce Bayesian PINN for hypocentre estimation problem through Laplace approximation, an approximation around the optimum/maximum a posteriori (MAP) PINN’s learnable parameters (weights).
  • To study the uncertainty propagation from the random initialization of PINN’s weights to the predictive solutions (e.g., Eikonal solution and hypocentre locations).
  • To investigate the influence of PINN’s loss landscape in quantifying the predictive uncertainty.

1. Deterministic Part: PINN’s Training & Prediction

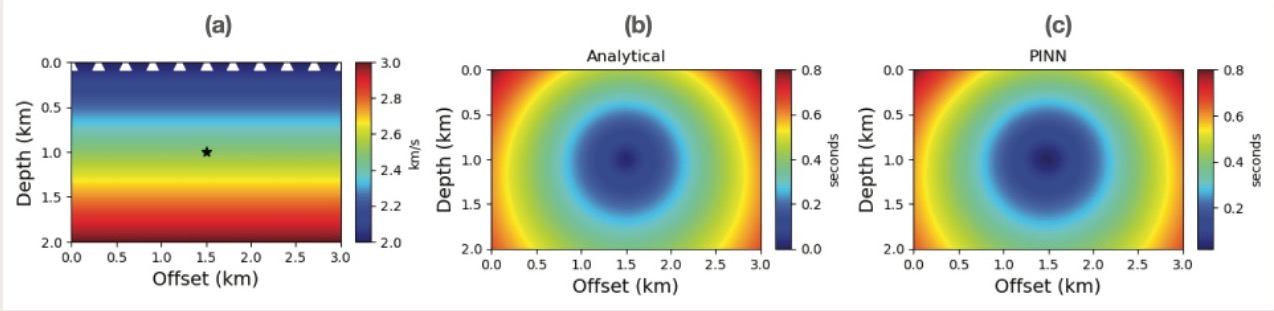
Figures_for_Research24_Izzat_Fig1

Figure 1. (a) Velocity model and real hypocentre location denoted by a black star. (b) The analytical Eikonal solution. (c) The Eikonal PINN solution with θ_{MAP}.


2. Bayesian Part: Quantifying predictive uncertainty in PINN

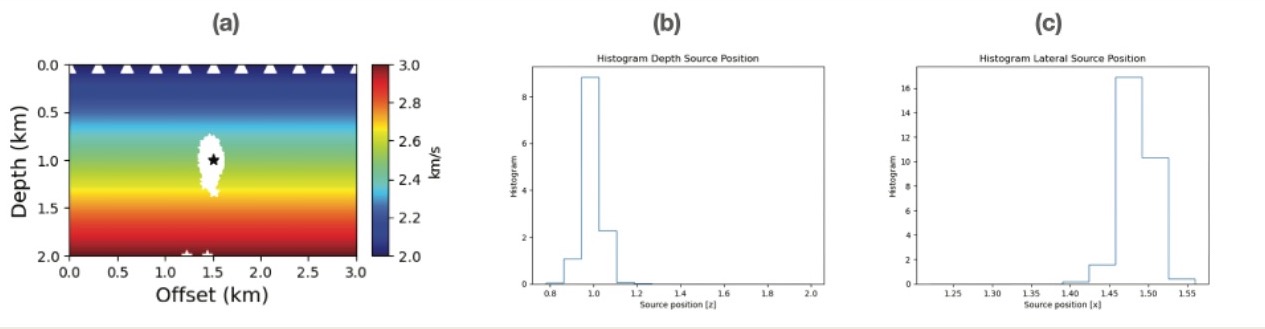
Figures_for_Research24_Izzat_Fig2

Figure 2. Predictive uncertainty of the locations of the hypocentre associated with weights’ realisations θ from Laplace approximation. (a) The locations of hypocentre associated with 1000 θ realisations from the Laplace approximation denoted by white stars. (b) The histogram of depth locations of the hypocentre realisations. (c) The histogram of lateral locations of hypocentre realisations.

 

Conclusions:

  1. Demonstrated the uncertainty estimation for Bayesian PINN which is similar as forward modelling uncertainty.
  2. The predictions of Eikonal solution and the hypocentre location vary significantly with different PINN’s weights realisation. This shows that the uncertainty in the PINN’s weights propagates into the predictive solution and significantly influences the prediction.
  3. The predictive uncertainty is sensitive to the PINN’s loss landscape.

 

Reference:

Izzatullah, M., Yildirim, I. E., Waheed, U. B., and Alkhalifah, T., 2022, "Predictive uncertainty quantification for Bayesian Physics-Informed Neural Network (PINN) in hypocentre estimation problem", submitted to the 83rd EAGE Annual Conference and Exhibition.

Izzatullah, M., Yildirim, I. E., Waheed, U. B., and Alkhalifah, T., 2022, "Predictive uncertainty quantification for Bayesian Physics-Informed Neural Network (PINN) in hypocentre estimation problem", submitted to the 83rd EAGE Annual Conference and Exhibition.