Optimal transport to a preconditioned data matching function for robust waveform inversion

Full-waveform inversion (FWI) promises a high-resolution model of the earth. It is, however, a highly nonlinear inverse problem; thus, we iteratively update the subsurface model by minimizing a misfit function that measures the difference between the measured and the predicted data. The conventional l2-norm misfit function is widely used because it provides a simple, high-resolution misfit function with a sample-by-sample comparison. However, it is susceptible to local minima if the low-wavenumber components of the initial model are not accurate.

Deconvolution of the predicted and measured data offers an extended space comparison, which is more global. The matching filter calculated from the deconvolution has energy focused at zero lag, like an approximated Dirac delta function, when the predicted data matches the measured one.

We have introduced a framework for designing misfit functions by measuring the distance between the matching filter and a representation of the Dirac delta function using optimal transport theory. We have used the Wasserstein W2 distance, which provides us with the optimal transport between two probability distribution functions. Unlike data, the matching filter can be easily transformed to a probability distribution satisfying the requirement of the optimal transport theory. Though in one form, it admits the conventional normalized penalty applied to the nonzero-lag energy in the matching filter, the proposed misfit function is metric and extracts its form from solid mathematical foundations based on optimal transport theory. Explicitly, we can derive the adaptive waveform inversion (AWI) misfit function based on our framework, and the critical “normalization” for AWI occurs naturally per the requirement of a probability distribution. We use a modified Marmousi model and the BP salt model to verify the features of the proposed method in avoiding cycle skipping. We use the Chevron 2014 FWI benchmark data set to further highlight the effectiveness of the proposed approach.

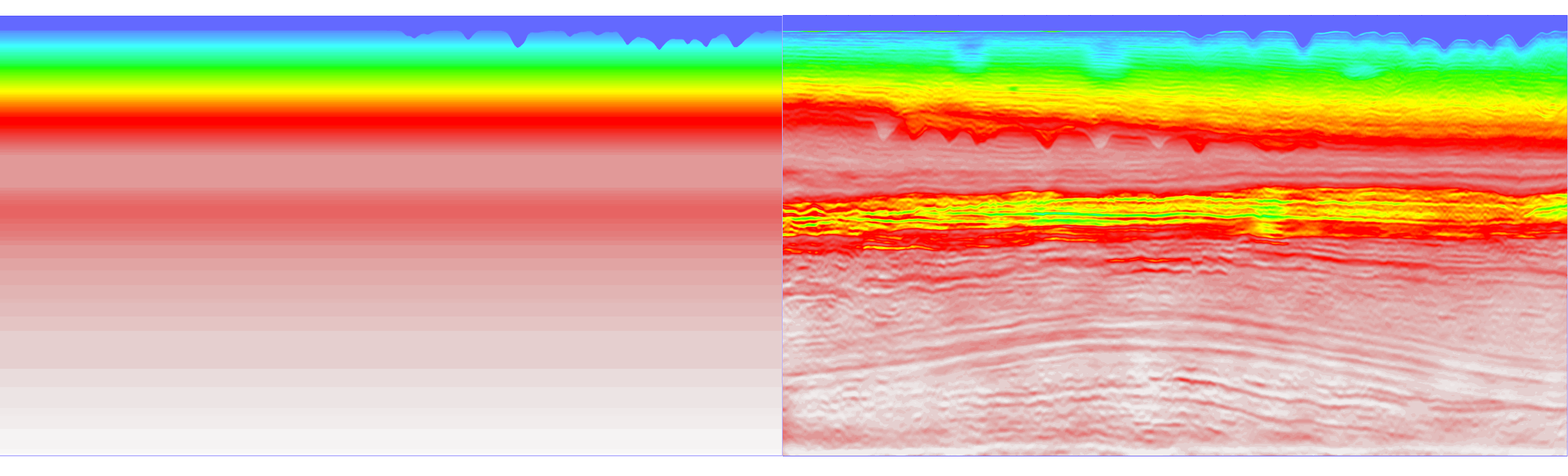The Chevron blind data initial model (left) and our inversion (right)

References

Sun B., and Alkhalifah T., (2019) "The application of an optimal transport to a preconditioned data matching function for robust waveform inversion", GEOPHYSICS, 84(6): R923–R945. DOI:10.1190/GEO2018-0413.1